本节课内容:
1、从逻辑回归引出支持向量机的原理
2、从直观上理解大间隔,及其数学原理
3、SVM核函数的定义、使用、含义、选择
4、探究逻辑回归和SVM算法的使用情景
优化目标
我们从逻辑回归开始,看看如何做一些小小的改动来得到一个支持向量机,在逻辑回归中,我们已经熟悉假设函数以及sigmoid激活函数,如果我们有一个样本,其中y=1,我们希望h(x)尽可能接近1,因为我们想尽可能正确的将样本分类,如果h(x)≈1,就意味着z远大于0, 同样,对于另一个y=0的样本,我们希望h(x)趋近于0,就意味着z远小于0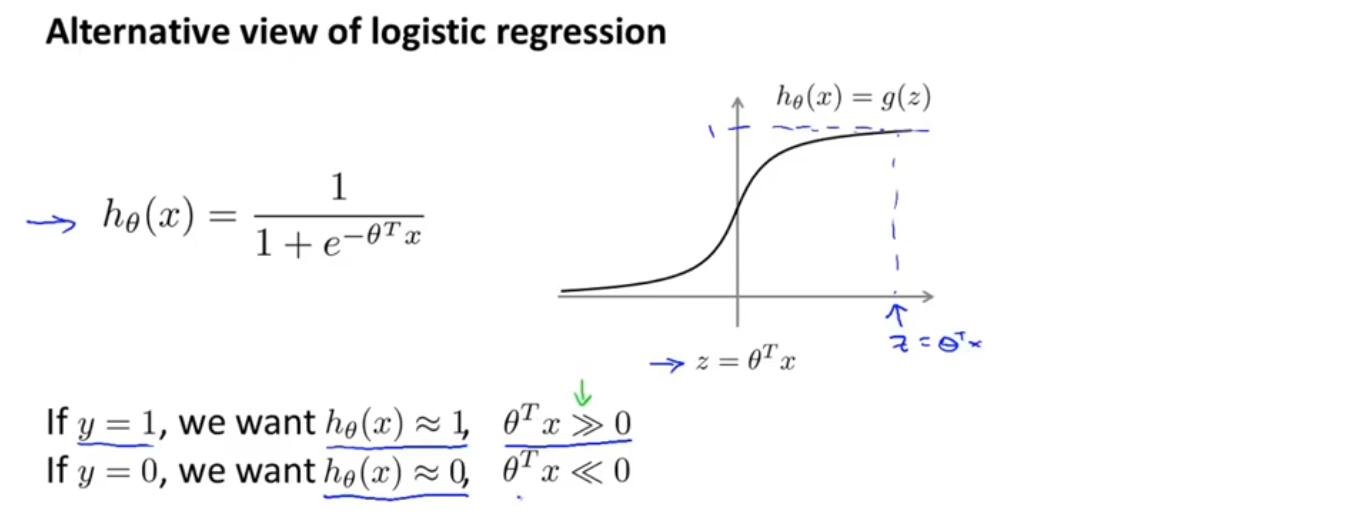
如果观察逻辑回归的代价函数,会发现每个样本(x,y)都会为总的代价函数增加这样一项,如下图蓝色箭头所示,如果将整个假设函数的定义带入其中,得到的就是每个样本对总体函数的具体贡献
现在考虑两种情况,一个是y=1的情况,一个是y=0的情况。在y=1的情况中,代价函数只有第一项起作用,如果绘制得到的代价函数与z的关系,会得到如图一的一条曲线,当z很大时,函数所对应的值会变得很小,也就是说它对代价函数的影响很小,这也就解释了为什么逻辑回归在看见y=1的样本时会将z设成一个很大的值,因为它在代价函数中的对应这一项的值很小
我们取z=1的点,绘制出新的代价函数曲线,在z=1点的右侧都是平的,代价函数值为0,左侧是与逻辑回归的代价函数曲线的趋势相似的一条直线,如图中粉色线,这就是当y=1时,我们要用到的代价函数cost_1,不难想象它和逻辑回归的效果很相似,事实上这会使支持向量机拥有计算上的优势,并使之后的优化问题变得简单,更容易解决
以同样的方法可以得到y=0时的新的代价函数曲线cost_0,如下图中的图二所示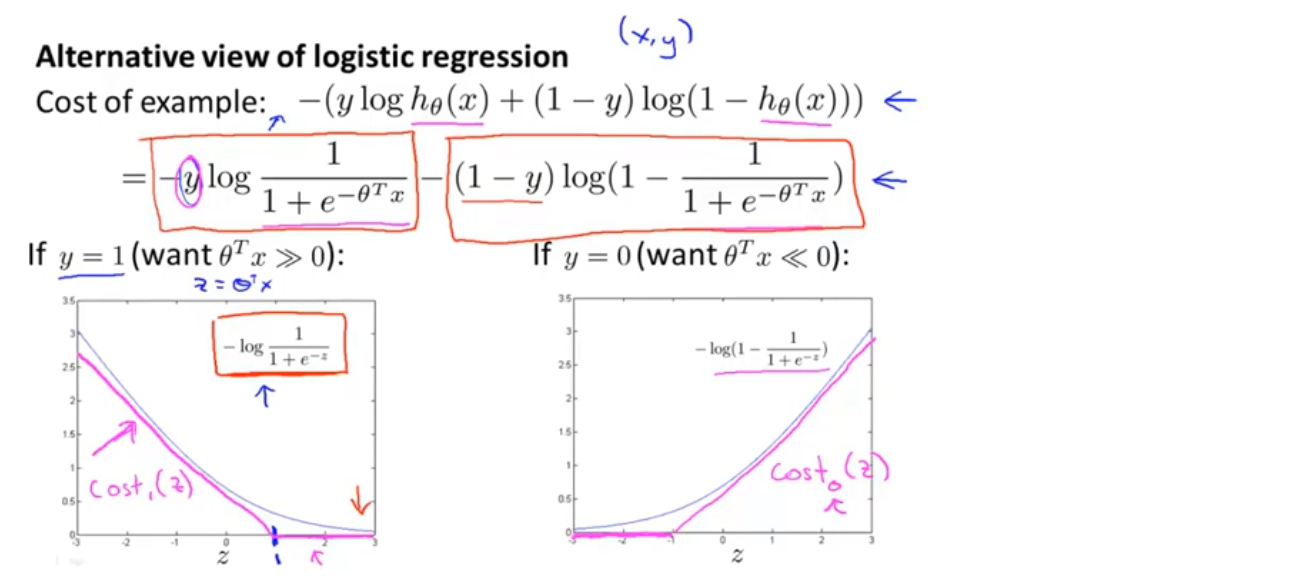
对于支持向量机而言,我们实际要做的是将代价函数J(θ)中相应的位置替换为cost_1(z)和cost_0(z),如下图所示
支持向量机中的一些东西的写法会略有不同,比如代价函数的参数会稍微有些不同,首先我们要去掉1/m这一项,因为在使用支持向量机和逻辑回归时,人们遵循的惯例略有不同,同样能得到θ的最优解
在逻辑回归中,我们的目标函数有两项,首先是训练样本的代价函数,其次是正则化项,要平衡这两项(A+λB),我们要做的是通过设定不同的正则化参数λ,以便能够权衡在多大程度上去适应训练集。对于SVM(支持向量机)而言,按照惯例我们会用一个不同的参数c,最小化cA+B,这只是一种不同的控制权衡的方式,或者说是一种不同的参数设置方法
最终我们得到了支持向量机的总体优化目标,如图中粉色箭头所示,当最小化这个函数时,就得到了SVM学习得到的参数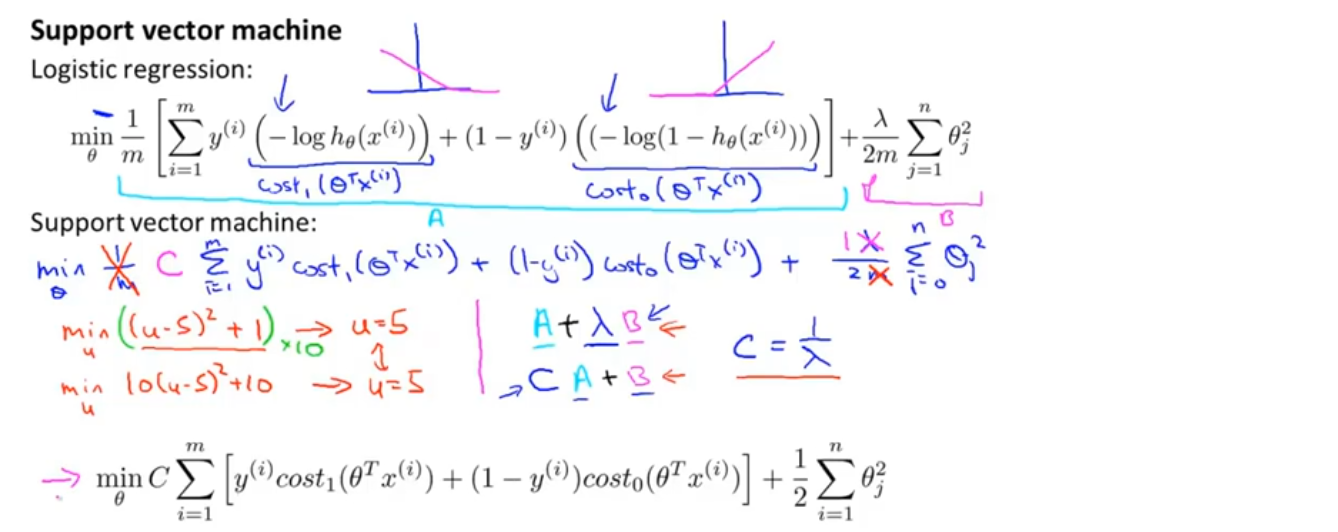
最后与逻辑回归不同的是,支持向量机并不会输出概率,相对的,我们得到的是通过优化这个代价函数得到一个参数θ,而支持向量机所做的是直接的预测,预测y=0或y=1,如果z≥0,那么假设函数就会输出1,反之会输出0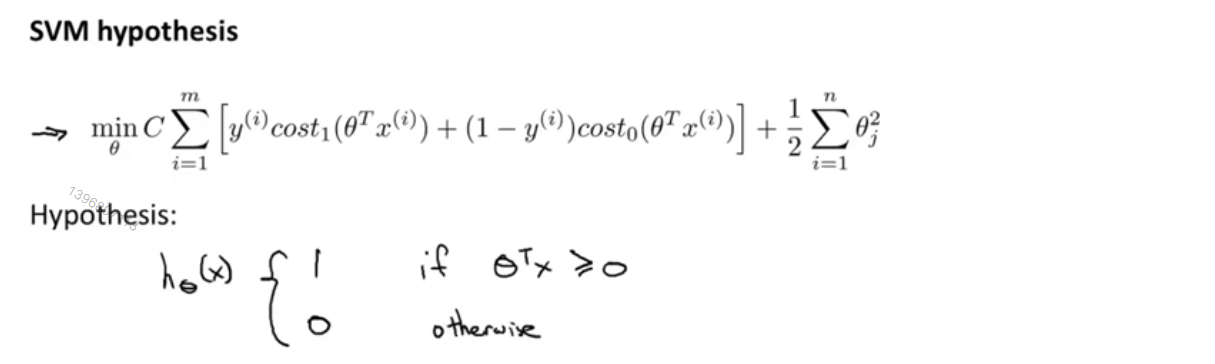
直观上对大间隔的理解
下图显示了支持向量机的代价函数,左侧的图为关于z的代价函数cost_1(z)的曲线,用于正样本,而右边是关于z的代价函数cost_0(z)的曲线,由于负样本。想象一些如何使这些代价函数变的更小,如果你有一个正样本,那么仅当z≥1时,有cost_1(z)=0;反之,若y=0,只有当z≤-1时,有cost_0(z)=0
这就相当于在支持向量机中构建了一个安全间距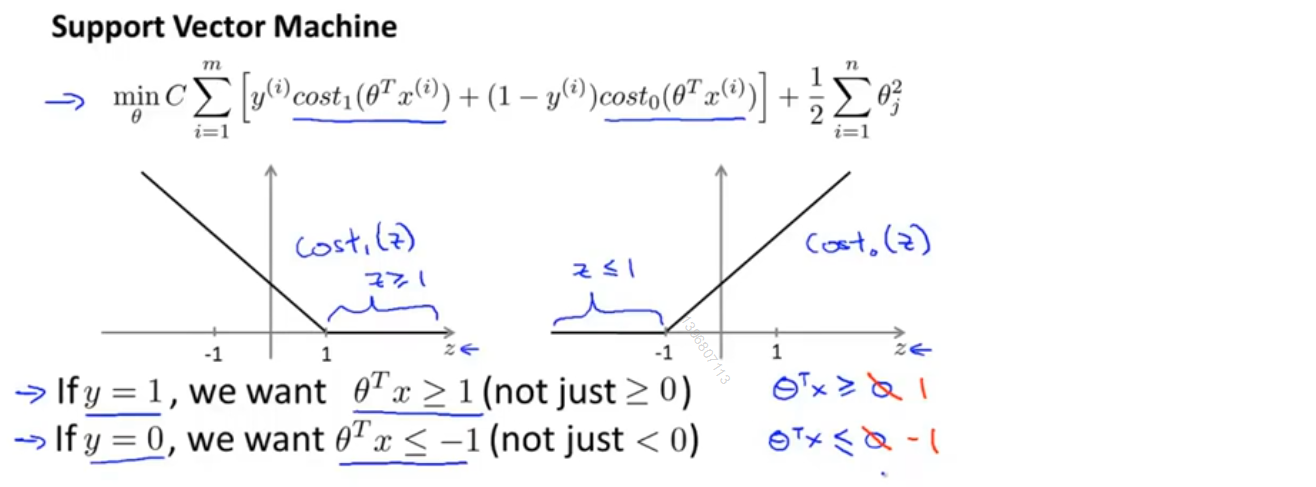
接下来考虑一种情况,我们常把常数c设成一个非常大的值,当最小化优化目标的时候,我们将迫切希望能找到一个值使得第一项等于0,要怎么做才能使第一项等于0?
当有一个y=1的训练样本,如果要使第一项为0,那么要找到一个θ值使得θ^T x^((i) )≥1,同样的当有一个y=0的训练样本,如果要使第一项为0,那么要找到一个θ值使得θ^T x^((i) )≤−1。因此如果把优化问题看作是通过选择参数来使第一项等于0,那么优化问题就变成了下面这样,如图中蓝色字所示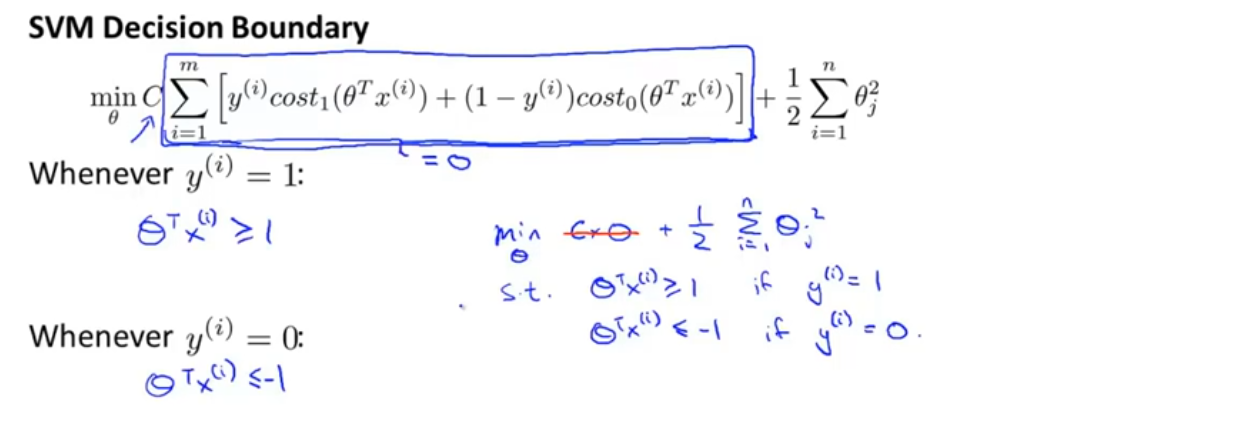
也就是说当解决这个优化问题的时候,会得到一个很有趣的决策边界
观察下图的数据集,其中有正样本和负样本,这些数据线性可分,SVM会选择图中黑色的直线作为边界,显然它比粉色和绿色的直线要好得多,能更好的分开正样本和负样本,从数学的角度说,这条黑色的边界拥有更大的距离,也就是,黑色的线和训练样本的最小距离要更大一些,这个距离被称为支持向量机的间距,这使支持向量机具有鲁棒性,因为它在分离数据时会尽量用最大的间距去分离,因此支持向量机有时被称为大间距分类器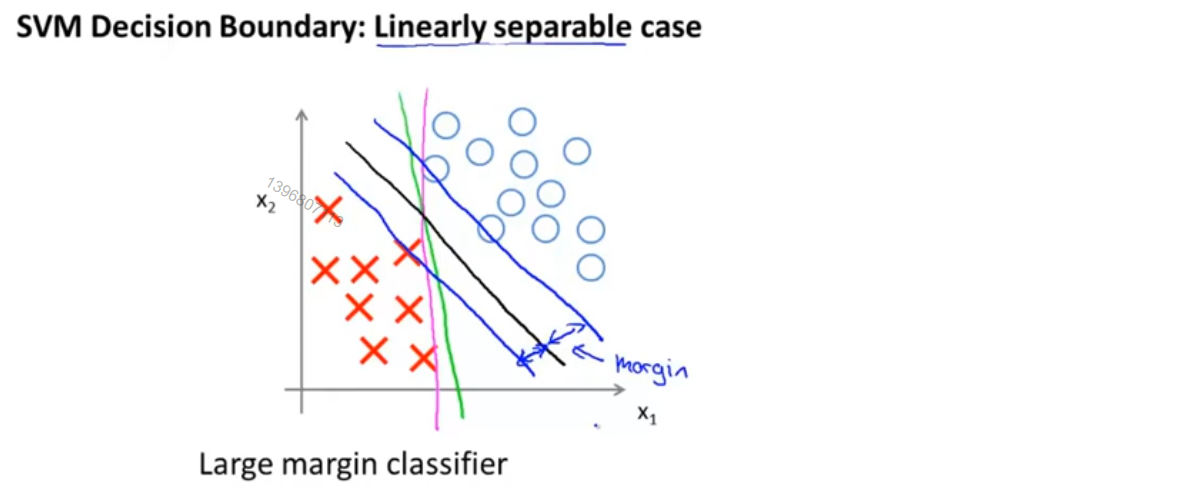
现在的大间距分类器是在常数c被设的非常大的情况下得出的,给定这样一个数据集,也许我们会选择如图中黑色直线这样的一条决策边界,用大间距来分开正样本和负样本,现在SVM实际上要比这个大间距的视图更加复杂,尤其是它对异常点会很敏感,我们加进去一个额外的正样本,为了将样本用大间距分开,最后学习得到的可能是如图中粉色线这样的一条决策边界,着这样一个异常点的影响下,只因为这一个样本就将决策边界从黑色的线变为了红色的线,这是c被设的非常大的情况,但如果c比较小,最后得到的还会是这条黑线,甚至当数据不是线性可分的时,SVM依然能够正确的分类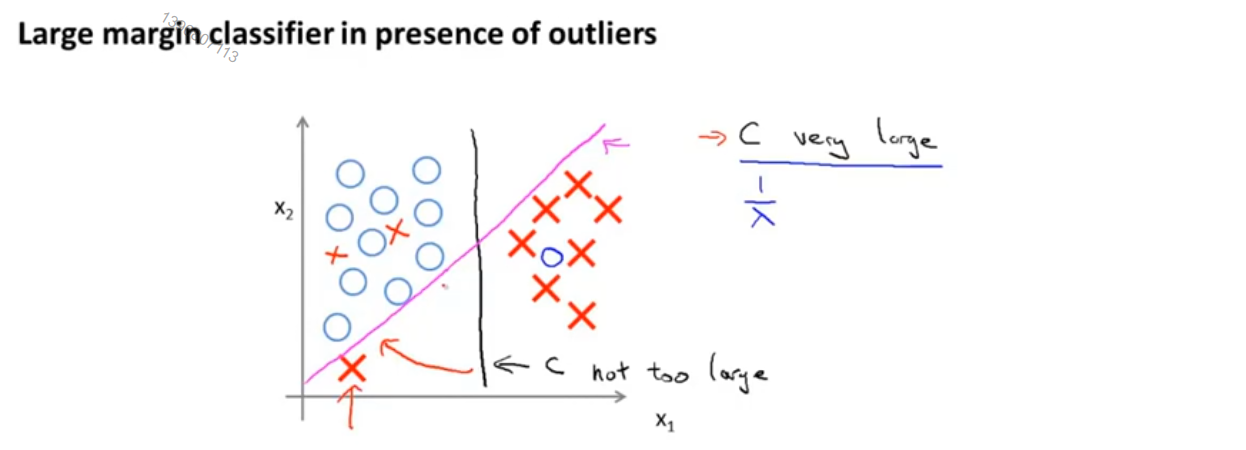
大间隔分类器的数学原理(选修)
首先将问题简化,我们假设θ_0=0,n=2
根据向量内积的性质,可以得出θ^T x^(i)=p^(i) ||θ||,其中,p^(i) 表示x^(i) 向θ的投影的长度(如果是负数,则表示两个向量间夹角大于90°),||θ||表示向量θ的长度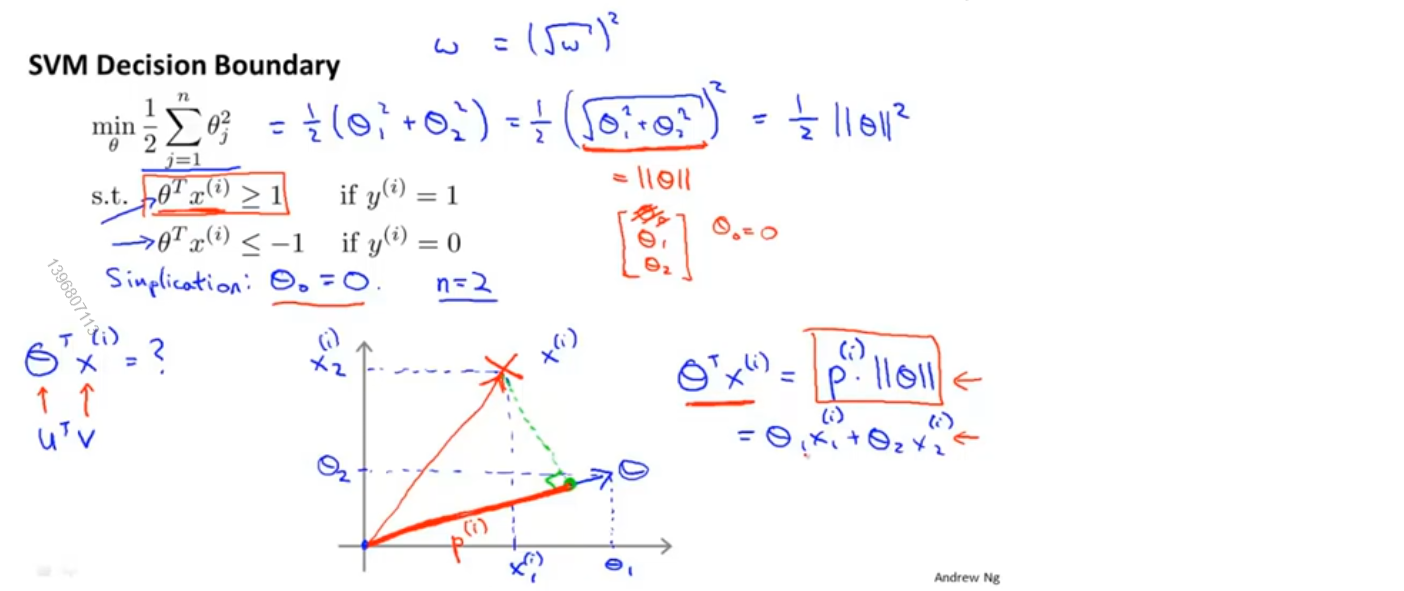
如下图所示,绿色直线为决策边界,由于θ_0=0,所以该直线是过原点的,θ所表示的向量与决策边界正交,即图中蓝色箭头
我们取任意样本向θ做投影,其中红色线段表示正样本的投影,粉色线段表示负样本的投影
如果是左图的决策边界,那么距离决策边界最近的正样本投影值会很小,为了让p^(i) ||θ||≥1,需要较大的||θ||,对于负样本也是如此;如果是右图的决策边界,尽量用较大的间隔去分离,只需要较小的||θ||,这就是SVM在做的事情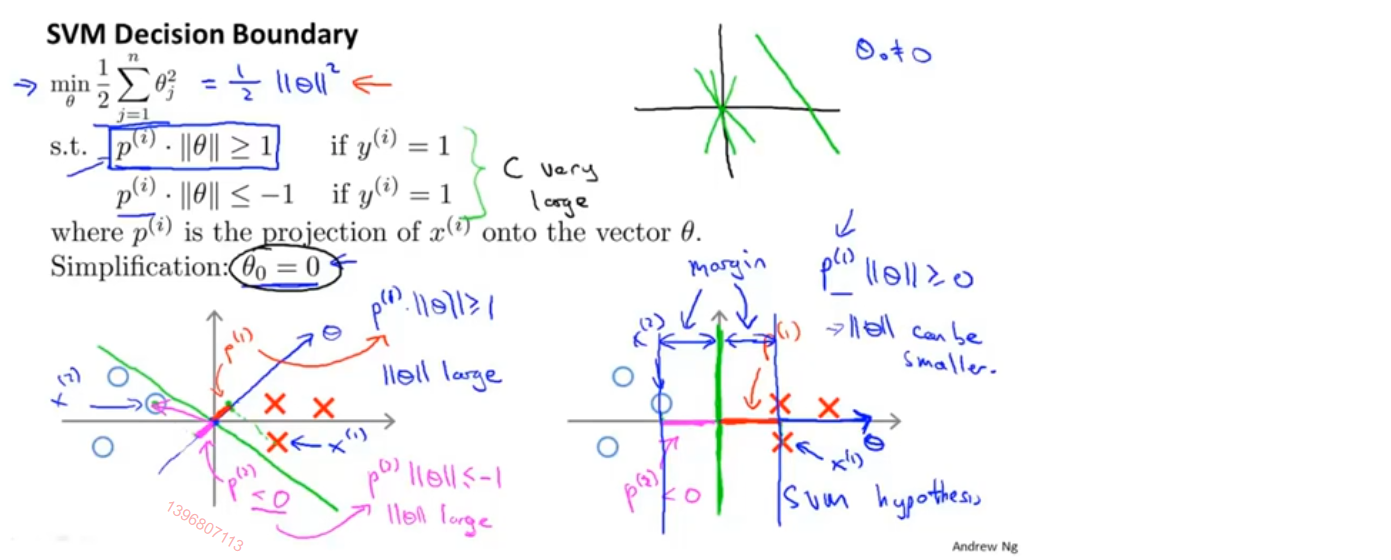
核函数
给出如下图所示的一个训练集,我们要拟合出一个非线性的决策边界,来区分正负样例,一种办法是构造复杂多项式特征的集合,得到一个如下图所示的这样的多项式,这里我们移入一个新的符号f,f_i 表示第i个特征,比如f_1=x_1,f_2=x_2,f_3=x_1 x_2 等,如果原始数据集中就有很多特征,那么得到的多项式特征将会非常非常多,这对计算来说是非常大的压力,是否还有更好的方法来选择特征呢?
构造新特征的方法
这里我们只构造三个新特征,对于特征x_1 、x_2,我们手动选取一些不同的标记点,比如l^(1)、l^(2)、l^(3),然后将新特征f_1 、f_2 、f_3 定义为一种相似度的度量,如图中蓝色字所示,即样本x与手动选取的点l^(i)的相似度similarity(x,l^(i)),这里的相似度就是核函数,这里使用的核函数实际上是高斯核函数,也可以使用不同的相似度核函数,核函数经常写作k(x,l^(i))
核函数到底做了什么
下图是刚刚用到的核函数,核心部分的分子是样本点x与标记点l^(i)的欧氏距离的平方,这里我们没有考虑x_0,x_0 总是等于1
假设x与其中一个标记点非常接近,那么两点间的欧式距离约等于0,核函数的结果就约等于1;假设x与其中一个标记点非常远,那么两点间的欧氏距离就会非常大,核函数的结果会接近于0
每一个标记点会定义一个新的特征,也就是说给定一个训练样本x,基于标记点,我们可以计算得到新的特征
我们将核函数画出来,如下图 所示,在三维图形中的高度表示核函数的结果,样本点位于下方的平面上,假设选取的标记点为(3,5),那么越接近这个标记点核函数的结果越接近于1,越远离这个标记点,核函数的结果越接近于0
此外σ是高斯核函数的参数,从图中我们也可以看出,当σ较大时,从标记点移走时,特征变量的值减小的速度较慢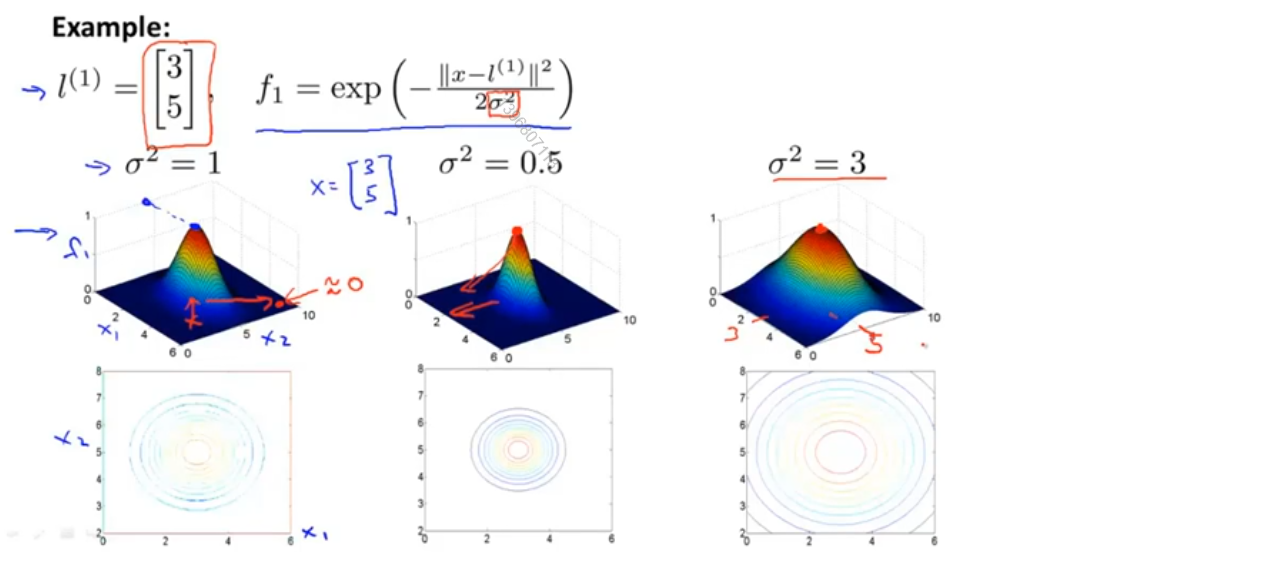
得到的预测函数
假设我们已经得到了θ参数的值,如下如图所示,我们就会得到一个预测函数
给定一个样本x,如图中粉色点,我们希望计算出它的y值,由于这个样本点很接近l^((1) ),又远离l^((2) ) 和l^((3) ),所以f_1 约等于1,f_2 、f_3 约等于0,最后多项式的结果大于等于0,预测y=1
再给定一个样本x,如图中浅蓝色点,该样本点远离l^(1)、l^(2)、l^(3),所以f_1 、f_2 、f_3 都约等于0,最后多项式的结果小于0,预测y=0
我们发现,对于接近于l^(1)、l^(2)的点,会预测y=1,对于远离l^(1)、l^(2)的点,会预测y=0,所以会得到红色线这样的决策边界,线内部预测y=1,线外部预测y=0
综上,我们可以由核函数和标记点来训练出非常复杂的非线性决策边界
如何获得标记点?
在实际的机器学习问题中,我们会不仅仅选取3个标记点,我们只需要直接将样本点作为标记点,使用这个方法,我们最终会得到m个标记点,即每一个标记点的位置都与每一个样本点的位置相对应,这说明特征函数基本上是在描述每一个样本距离
我们来具体描述一下这个过程:
1、给定一个包含m个数据的训练集,将每个样本点都选做标记点,得到m个标记点
2、给定一个样本x^(i),这个样本可以来自于训练集、测试集、验证集,计算该样本点与m个标记点的相似度,作为该样本点新的特征向量f^(i),其中f_0^(i)=1,由于l^(i)=x^(i),因此f_i^(i)=1
3、使用新的特征向量f^(i)作为样本进行训练
在实际使用支持向量机进行训练时,最后一项可能会稍作变化,使其可以应用到更大的数据集上,并得到更高的效率
如何选择支持向量机中的参数?
支持向量机中,参数c的作用与λ类似,λ是逻辑回归中的正则化参数。当c较大时,对应着逻辑回归中λ较小的情况,这意味着不使用正则化,可能得到一个低偏差高方差的模型,更倾向于过拟合;当c较小时,则可能得到高偏差低方差的模型,更倾向于欠拟合
另一个要选择的参数是高斯核函数中的σ。当σ偏大时,相对应的相似度函数倾向于平滑,变化比较平缓,这会给模型带来较高的偏差和较低的方差;反之当σ较小时,相似度函数会变化的很剧烈,会给模型带来较低的偏差和较高的方差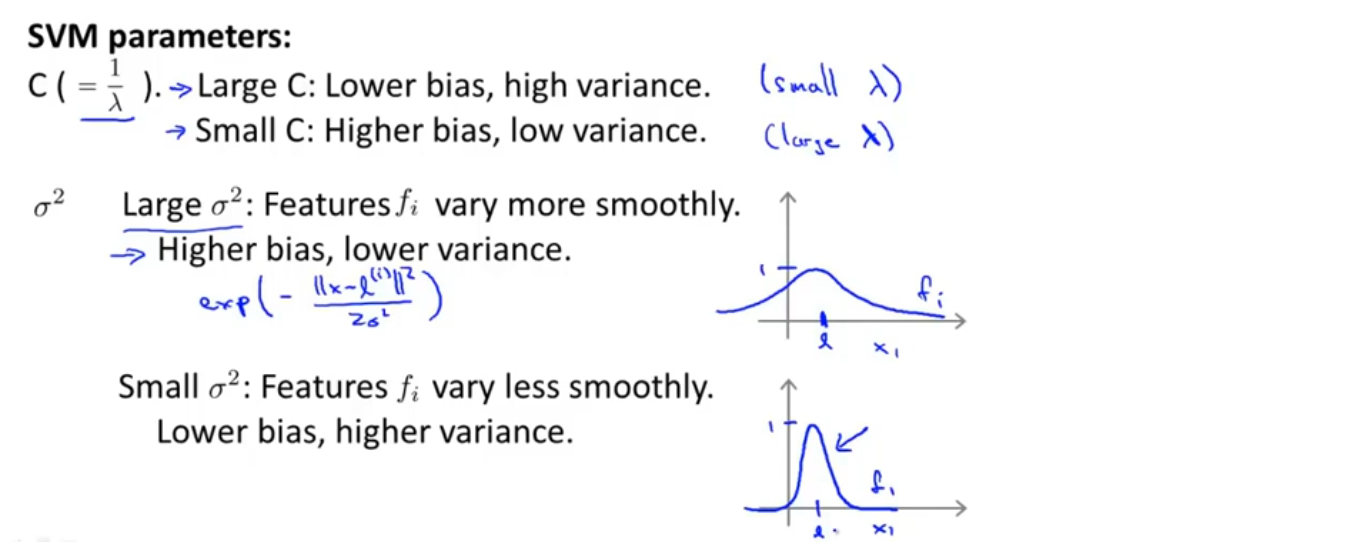
使用SVM
我们不需要自己动手实现SVM的算法,但需要选取参数和核函数
一种常用的是不使用核函数,也就是线性SVM,如果有大量的特征,但训练的样本数很少,可能只想拟合一个线性的决策边界,而不是特别复杂的多项式决策边界,因为训练样本太少,可能会过拟合
另一种常用的核函数是高斯核函数,使用高斯核函数还需要选取参数σ,如果我们的训练集的特征较少,而训练样本数量很多,可能会想拟合一个比较复杂的非线性决策边界,可以选择高斯核函数。此外,如果选用高斯核函数,必要的情况下需要对原始特征变量进行缩放
不论使用什么核函数都需要满足一个技术条件,叫做默塞尔定理,这个定理所做的就是确保所有的SVM软件包都能用大类的优化方法从而迅速得到参数θ
还有另外一些不常用的核函数,比如多项式核函数以及一些更复杂的核函数,多项式核函数通常都要求x和l都是严格非负的,这样可以保证x和l的内积永远不会是负数,从而当x和l很接近时,内积也会很大
逻辑回归与SVM的选择
假设n代表训练集的特征数量,m代表训练集的样本数量
如果n很大,n=10000+,m较小,m∈(10,1000),使用逻辑回归或者线性SVM
如果n较小,n∈(1, 1000),m大小适中,m∈(10,10000),使用高斯核函数的SVM
如果n较小,n∈(1, 1000),m很大,m=50000+,这时高斯核函数将会计算的很慢,可以手动创建更多的特征变量,然后使用逻辑回归或者线性SVM
逻辑回归和线性SVM是很相似的算法,在其中一个算法应用的问题中,另一个算法可能也很有效
最后对于所有的这些问题,设计不同的神经网络可能会非常有效,但有时不会使用神经网络的原因是,对于许多问题,神经网络训练起来可能会特别慢。此外,SVM具有的优化问题,是一种凸优化问题,SVM包总会找到全局最小值或者接近它的值,因此对于SVM不用担心局部最优,但实际在神经网络中,局部最优是一个不大不小的问题
课程资料
课程原版PPT-Support Vector Machines
练习内容和相关说明
相关数据ex3data1
python代码实现
1-linear-SVM.ipynb
2-Gaussian-kernels.ipynb
3-search-for-the-best-parameters.ipynb
4-spam-filter.ipynb
ML-Exercise6.ipynb