本节课内容:
1、介绍非线性假设,逻辑回归方法的局限性
2、讲解神经网络的来源、理念、模型
3、简单介绍神经网络的多元分类
非线性假设
给定如图所示的数据集,我们可以构造包含许多非线性项的逻辑回归函数,当多项式数量足够多时,就可以分开正样本和负样本的假设。当只有两个特征时,可以将x1,x2的所有组合都包含进多项式中,但大多数机器学习问题的特征远不止两项(e.g. n=100),这时,如果要多项式中包含所有的项,即使只包含二次项,最终也会有很多项。
因此要包含所有的二次项,并不是一个好方法,由于包含的项数太多,最终可能导致过拟合问题,而且处理这么多项也存在运算量过大的问题。
当然也可以取二次项的子集,如只包含平方项,项的数量会明显减少,但最终不会得到理想的结果,因为忽略了太多相关项

e.g. 在计算机视觉中,每个像素点看作一个特征,假设一个50x50的灰度图片,就包含2500个特征(如果是RGB图片则包含7500个特征),如果用逻辑回归,那么多项式中要包含3百万个项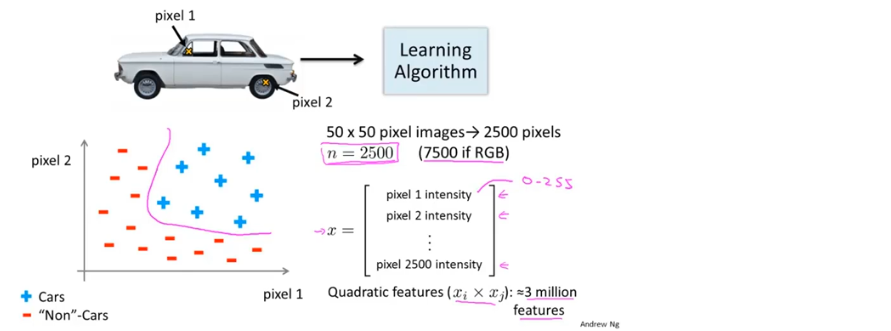
神经元与大脑
神经网络:起源:人们想尝试设计出模仿大脑的算法,它的理念是如果我们要建立学习系统,要去模仿我们所认识的最神奇的学习机器,人类的大脑
神经网络兴起于20世纪八九十年代,应用的非常广泛,但由于各种原因,90年代的后期就应用的很少了,但最近神经网络又再度兴起,原因之一是神经网络的计算量较大,近些年计算机的运行速度变快,才足以运行大规模的神经网络
神经重接实验:如果有一块脑组织可以处理光、声或触觉信号,那么也许存在一种学习算法,可以同时处理视觉、听觉和触觉,而不是需要运行上千个不同的程序,或者上千个不同的算法来做这些,也许我们需要做的就是找出一些近似的或实际的大脑学习算法,然后实现它,让大脑自己学习如何处理这些不同类型的数据
模型展示(一)
大脑中的神经细胞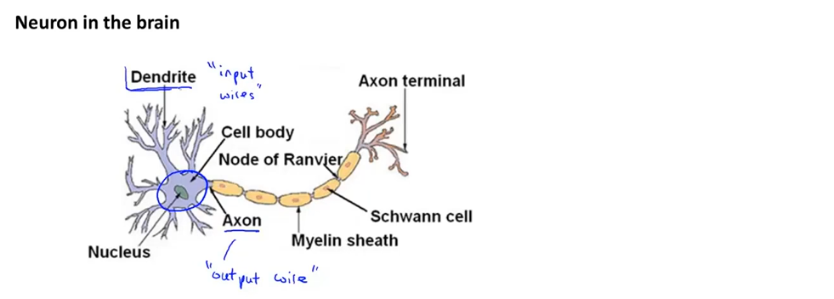
在一个人工神经网络里,我们使用一个很简单的模型来模拟神经元的工作,我们将神经元模拟成一个逻辑单元(图中黄色圆圈),通过输入通道传递给它一些信息,然后神经元做一些计算,再通过输出通道输出计算结果
x_0称为偏置单元或偏置神经元,非线性函数g(z)称为激活函数,θ称为模型参数或权重
神经网络是一组神经元连接在一起的集合
神经网络的第一层称为输入层,在这一层输入特征;最后一层称为输出层,这一层输出最终计算结果;中间第二层称为隐藏层,隐藏层的值在训练集中是看不到的,神经网络可以有不止一个隐藏层,实际上任何非输入层和非输出层都成为隐藏层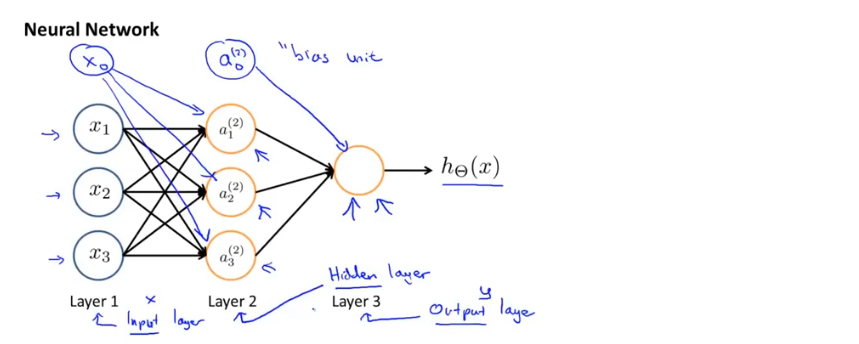
在神经网络中,a_i^((j)) 表示第j层第i个神经元或单元的激活项,激活项是指由一个具体神经元计算并输出的值
一般地,如果一个神经网络,在第j层有s_j个单元,在第j+1层有s_(j+1)个单元,Θ^((j)) 即控制第j层到第j+1层映射的矩阵,它的纬度为s_(j+1)*(s_j+1)
总结:神经网络定义了函数h,从输入x到输出y的映射,这些假设被参数化,记做Θ,因此只要改变Θ就能得到不同的假设
模型展示(二)
前向传播:从输入单元的激活项开始,然后进行向前传播给隐藏层,计算隐藏层的激活项,继续向前传播,计算输出层的激活项,这个依次计算激活项,从输入层到隐藏层再到输出层的过程叫做前向传播
下图中右侧为前向传播公式的向量化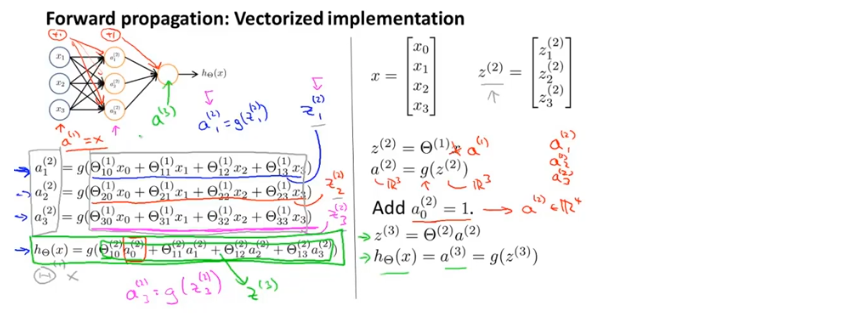
在下图的神经网络中,将左侧输入层临时遮住,图中剩下的部分很像标准的逻辑回归,但输入该逻辑回归的特征是通过隐藏层计算的新的特征a,而不是原本的特征x
在神经网络中,新的特征项a是学习得到的函数输入值,即从第一层映射到第二层的函数,这个函数由参数Θ^((1)) 决定,因此在神经网络中没有用特征x做逻辑回归,而是训练逻辑回归的输入a,根据为Θ^((1)) 选择不同的参数,可以学习到一些有趣和复杂的特征,得到更好的假设函数,比使用原始特征x得到的假设更好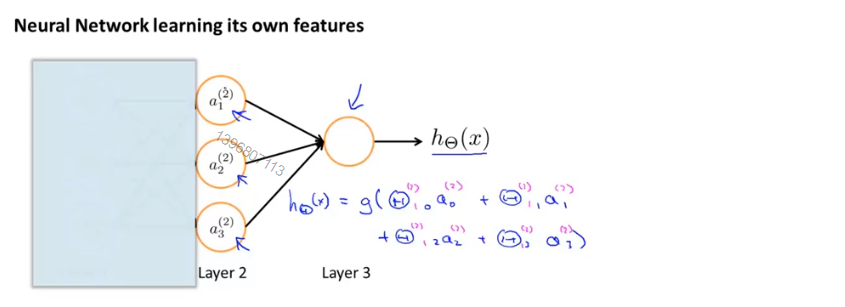
神经网络中神经元的连接方式称为神经网络的架构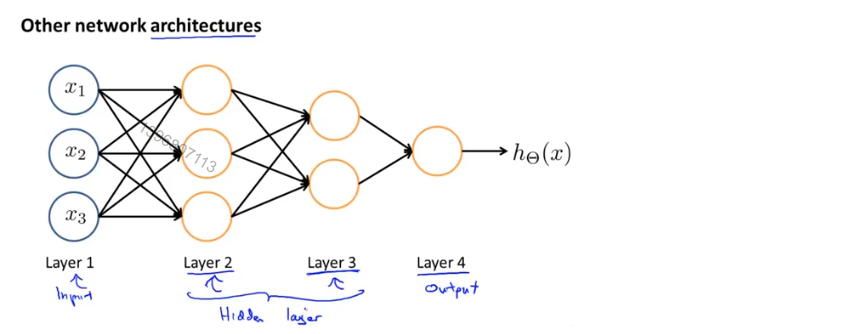
例子与直觉理解(一)
神经网络中的单个神经元用来计算逻辑函数
下图中左侧为右侧问题的简化版,是XNOR运算的训练集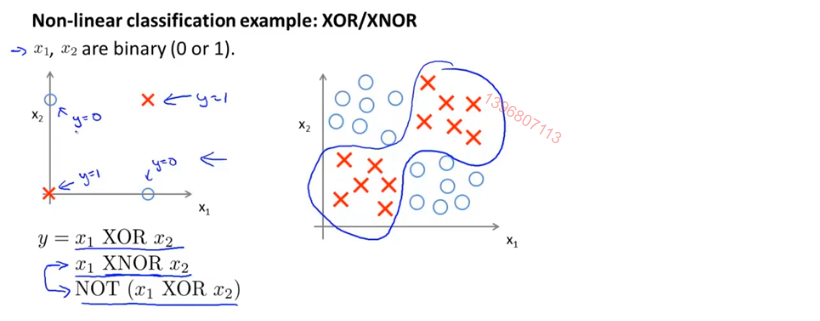
要构建神经网络拟合XNOR运算,要先从比较简单的能够拟合AND运算、OR运算和NOT运算的神经网络入手,下图是AND运算的神经网络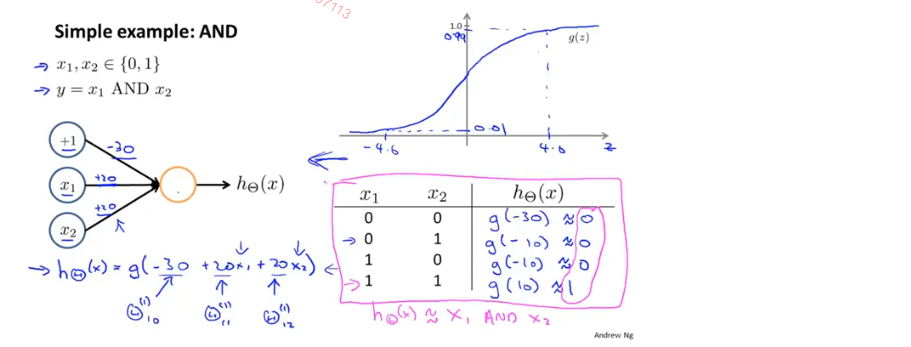
例子与直觉理解(二)
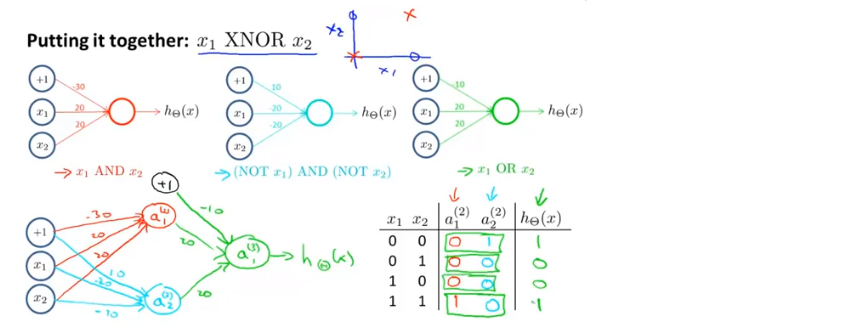
将输入放在输入层,中间放一个隐藏层用来计算一些关于输入的略微复杂的功能,然后再继续加一层用来计算一个更复杂的非线性函数
当神经网络有许多层,在第二层中有一些关于输入的相对简单的函数,第三层又在此基础上计算更加复杂的方程,再往后的层次计算的函数越来越复杂
多元分类
如下图所示的神经网络要来识别图片中的物体,在输出层中,4个分类器每个都将识别图片中的物体是否是四种分类中的一种,即四输出单元的神经网络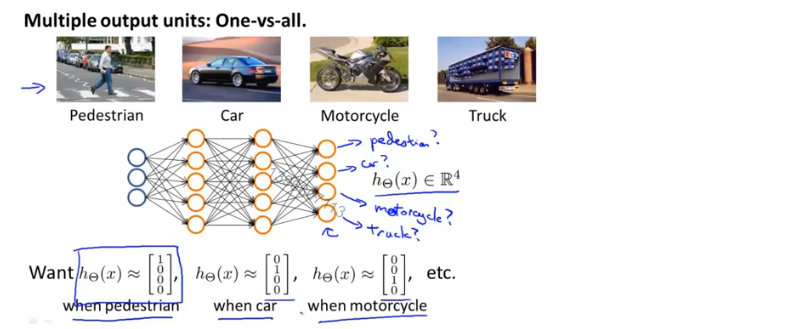
之前我们用整数y作为输出的分类标签,现在用向量y^(i)作为输出结果,y^(i)的值取决于对应的图像x^(i),因此,一个训练样本由一组(x^(i), y^(i))组成,其中x^(i)是四种物体其中一种的图像,y^(i)是结果向量中的一个,我们要找到一些方法让神经网络输出一些数值,输出值h(x^(i))等于y^(i),并且h(x^(i))与y^(i)在本例子中都是四维向量,分别代表不同的类别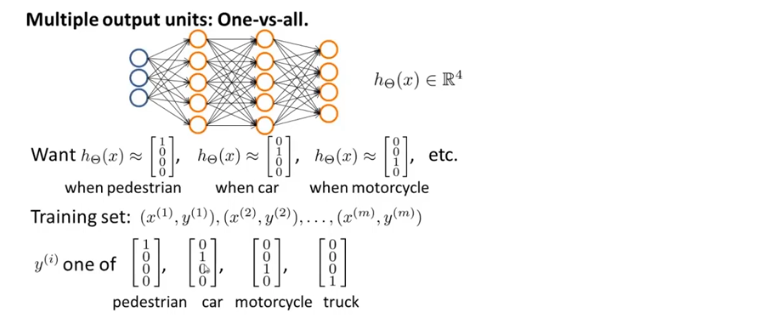
课程资料
课程原版PPT-Neural Networks: Representation
练习内容和相关说明
相关数据ex3data1,相关数据ex3weights
python代码实现
1.neural_network.ipynb
ML-Exercise3.ipynb
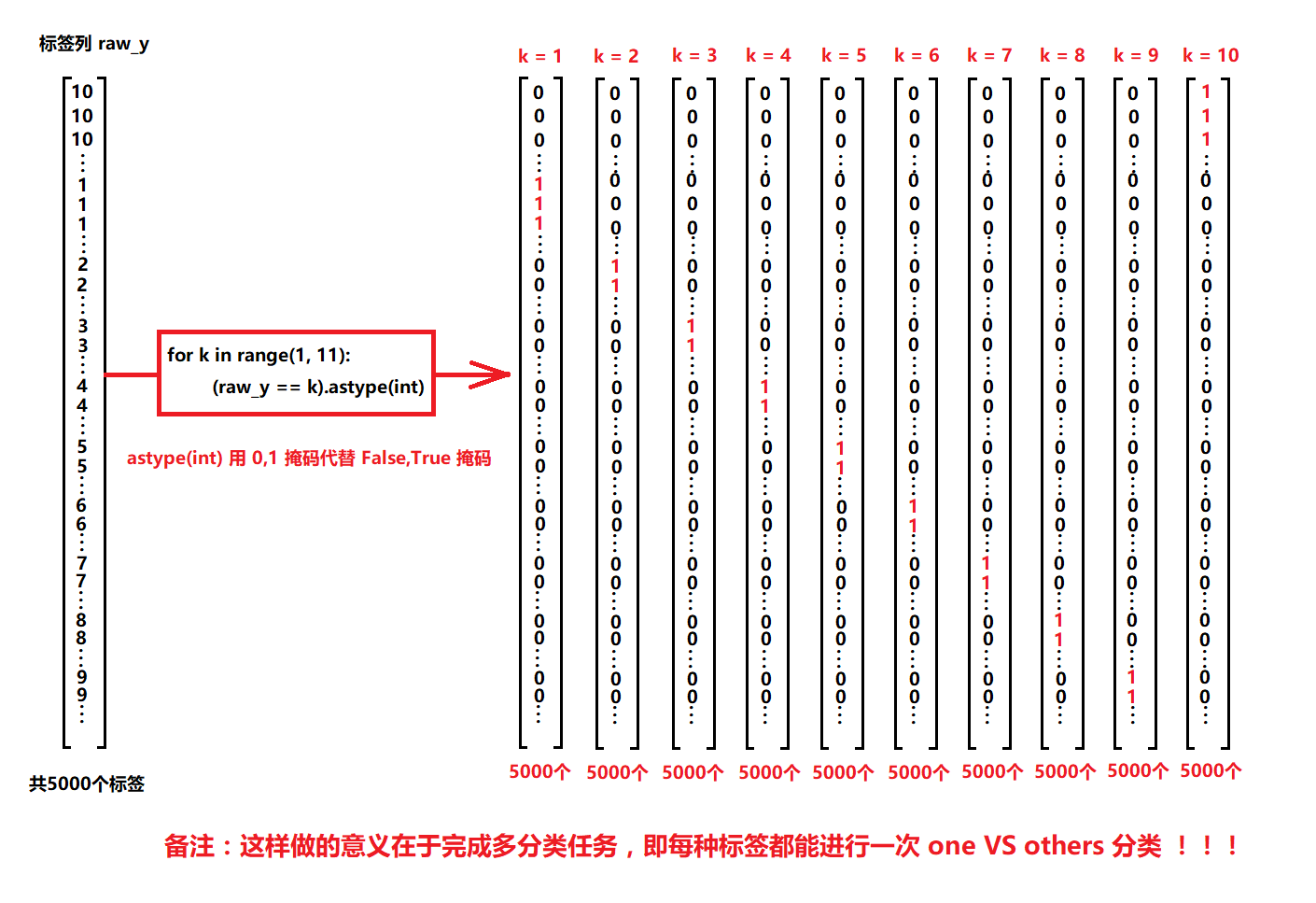
向量化标签