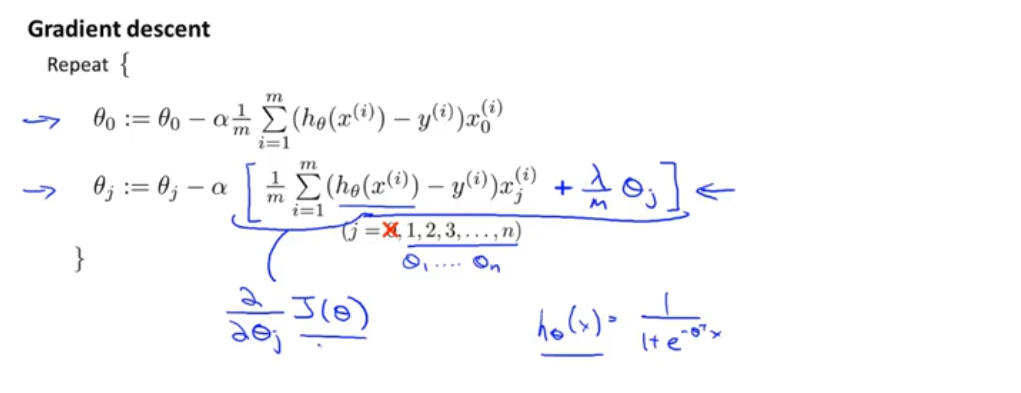本节课内容:
1、介绍什么是欠拟合和过拟合
2、介绍过拟合问题的解决方法——正则化
3、介绍线性回归和逻辑回归中,正则化的应用
过拟合问题
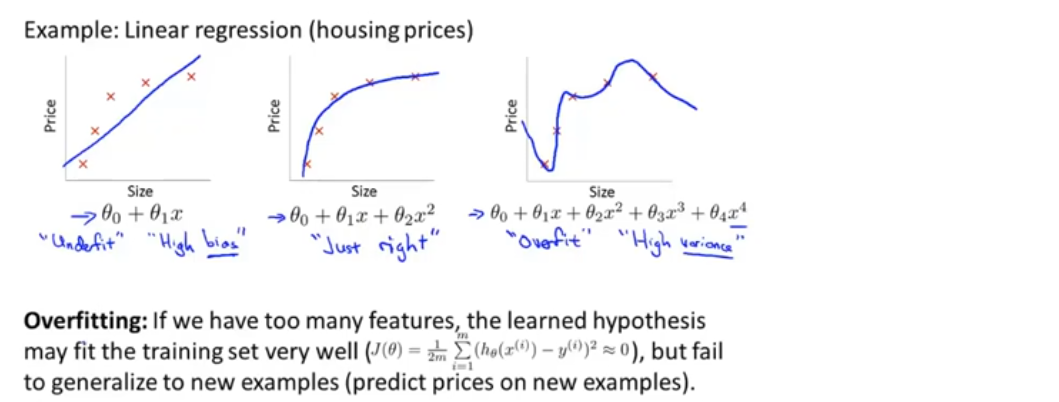
以估计房屋价格的问题为例,给定一些数据(如下图所示),随着size的增大,房屋的价格是趋于稳定的
如果用直线来拟合数据(左图),和这样的趋势不相符,所以不能很好的拟合训练数据,这个问题称为欠拟合(underfit),或称算法具有高偏差(high bias)
如果用二次函数拟合数据(中间图),拟合效果很好
另一种极端情况(右图),拟合一个四阶多项式,这似乎很好的拟合了数据集,因为图像经过了所有的数据点,但这是一条扭曲的曲线,不停的上下波动,我们不认为这是一个预测房价的好模型,这个问题称为过拟合(overfit),或称算法具有高方差(high variance)
过拟合(Overfitting):过拟合问题会在变量过多的时候出现,这时训练出的假设函数(hypothesis)能很好的拟合训练集(代价函数可能非常接近0),它千方百计的拟合训练数据集,导致无法泛化到新的样本中
泛化:指一个假设模型应用到新样本的能力
同样的问题也存在于逻辑回归中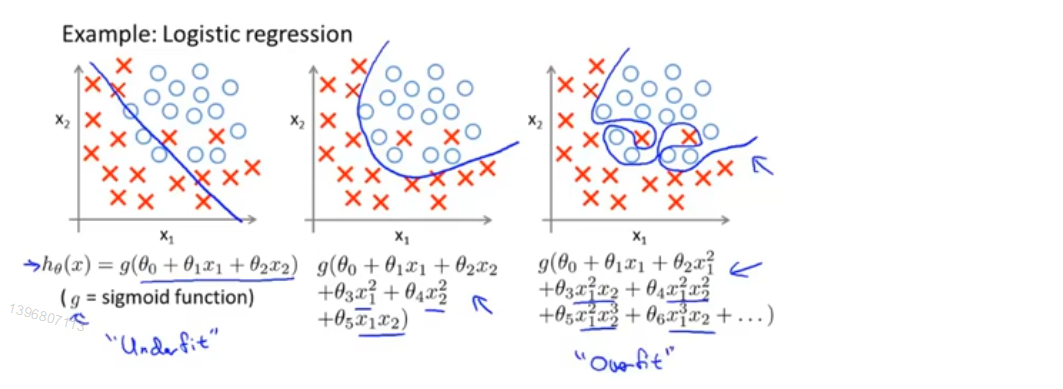
解决过拟合问题
当我们使用一维或二维数据时,可以通过绘制出假设模型的图像来研究问题。但实际应用中,机器学习问题需要很多变量,这不仅仅是选择多项式阶次的问题,当我们有很多特征变量时,绘图会变得更难,通过数据可视化来决定哪些特征变量也会更难
如果有很多特征变量,而只有非常少的训练数据时,就会出现过拟合问题
有两个办法解决问题:
1、减少选取变量的数量:
- 人工检查变量清单,并决定哪些变量更重要,哪些特征应该保留,哪些应该舍去
- 模型选择算法,自动选择哪些变量保留,哪些舍弃
缺点:舍弃一些特征变量的同时,也舍弃了关于问题的一些信息
2、正则化:
- 保留所有特征变量,但减少量级或参数θ_j 的大小
- 当有许多特征变量,且每个特征变量都对预测y值有影响时 ,效果很好
代价函数
向代价函数中加入惩罚项,使得θ_3,θ_4 都非常小(如下图所示)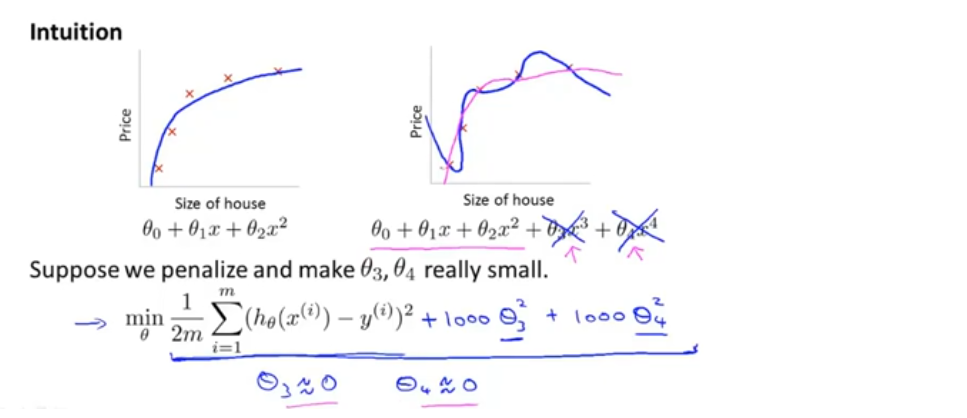
正则化:如果参数值较小,意味着更简单的假设模型(越平滑),更不容易出现过拟合问题
e.g.假设给定一个数据集中有很多特征变量(m个),我们并不知道那个参数对应高阶项,对于m个特征,我们也很难选出其中哪个变量是相关度较低的,也就是有n个参数θ,很难选出哪些参数来缩小它的值,我们要做的就是修改代价函数来缩小所有参数(没有对θ_0 添加惩罚项,这是约定俗成的,实际上无论从θ_0 开始,还是θ_1 开始,对结果影响都不大)
λ为正则化参数,作用是控制两个不同目标之间的平衡关系。第一个目标与目标函数的第一项有关,即更好的拟合训练数据;第二个目标是保持参数尽量小,与目标函数第二项(正则化项)有关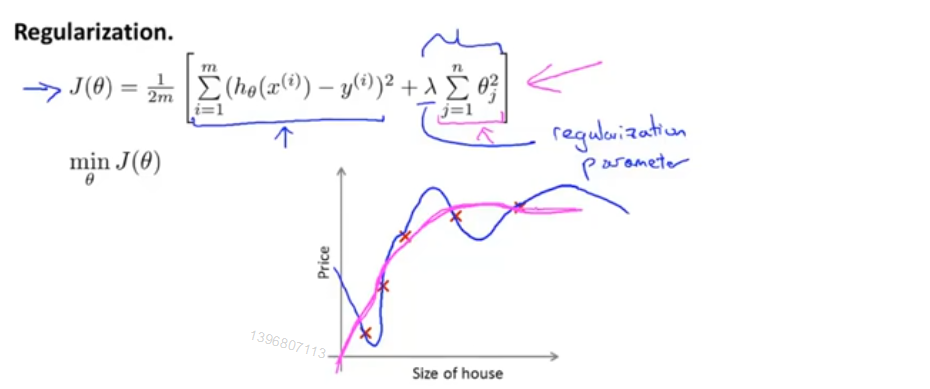
在正则化线性回归中,如果正则化参数λ被设置的太大,结果就是对参数的惩罚程度太大,会导致参数都接近于0,相当于把假设函数的全部项都忽略掉了,最后假设模型只剩下h(x)=θ_0,这就导致欠拟合
因此,为了让正则化起到效果,要选择更合适的正则化参数λ
线性回归的正则化
梯度下降
将θ_0 单独分离出来(正则化从θ_1 开始)
在正则化的梯度下降中,每一次迭代,θ_j 都会乘一个比1略小的数,也就是θ_j 每次迭代都会缩小一点点,然后进行和之前一样的更新操作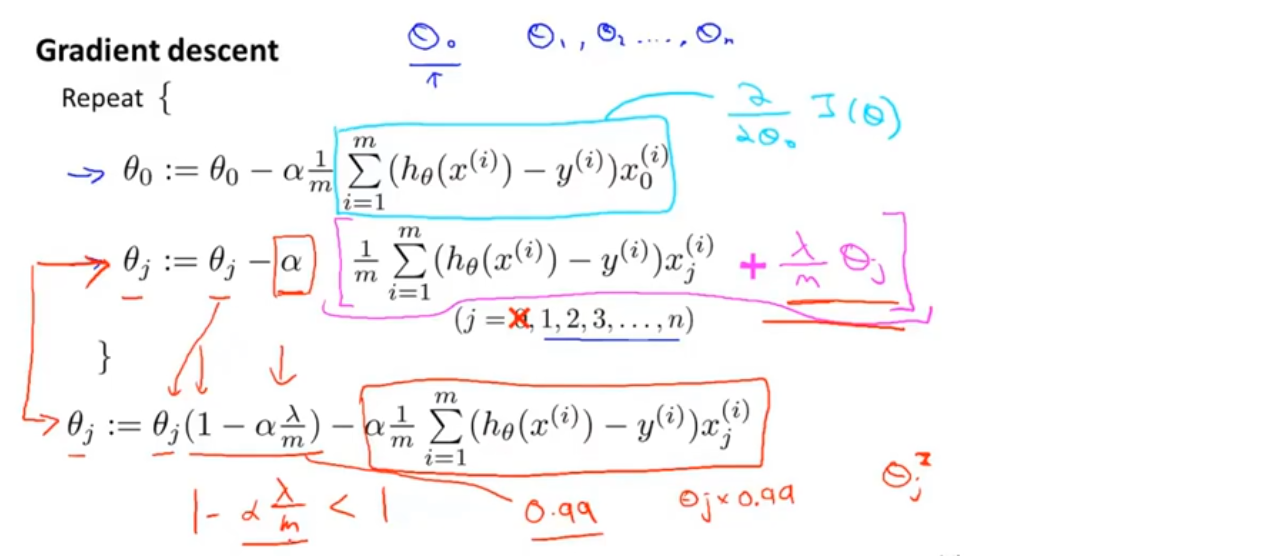
正规方程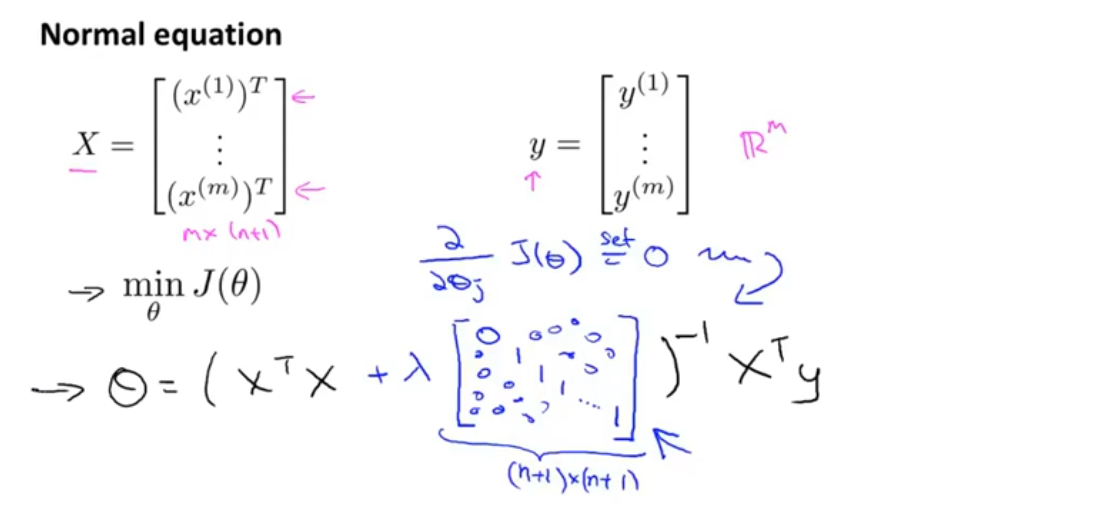
对于X’X矩阵是否可逆的问题:在正规方程的正则化中,只要λ是严格大于0的,就可以确信公式中括号内的矩阵一定是可逆矩阵,因此正则化还可以解决X’X出现不可逆的问题
逻辑回归的正则化