本节课内容:
1、介绍分类问题,并用逻辑回归解决分类问题
2、介绍逻辑回归的决策边界,假设函数(hypothesis),代价函数,以及用梯度下降法求解最优θ值
3、介绍高级优化方法,及其在octave中的实现
4、介绍多分类问题(一对多,一对余),以及解决多分类问题的基本思想
分类
y的取值是离散的
二分类问题中,yϵ{0,1},0表示“负类”,1表示“正类”,在两个类别中,哪个是正类哪个是负类并没有什么区别,但一般来说,负类表示没有某样东西
给定一个分类问题的训练集(如下图所示),如果用线性回归的方法对数据进行拟合,会得到一个分界点,其左侧预测为0,右侧预测为1,在这个数据集上,线性回归的结果似乎是可行的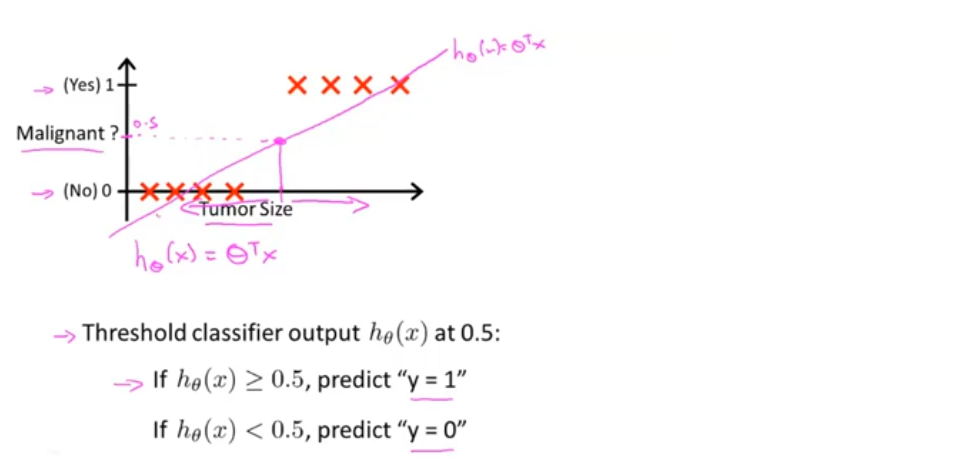
假设数据集改变,如下图所示,此时,如果再用线性回归来拟合数据,会得到一条新的直线,分界点也会随之改变,其左侧预测为0,与原数据不相符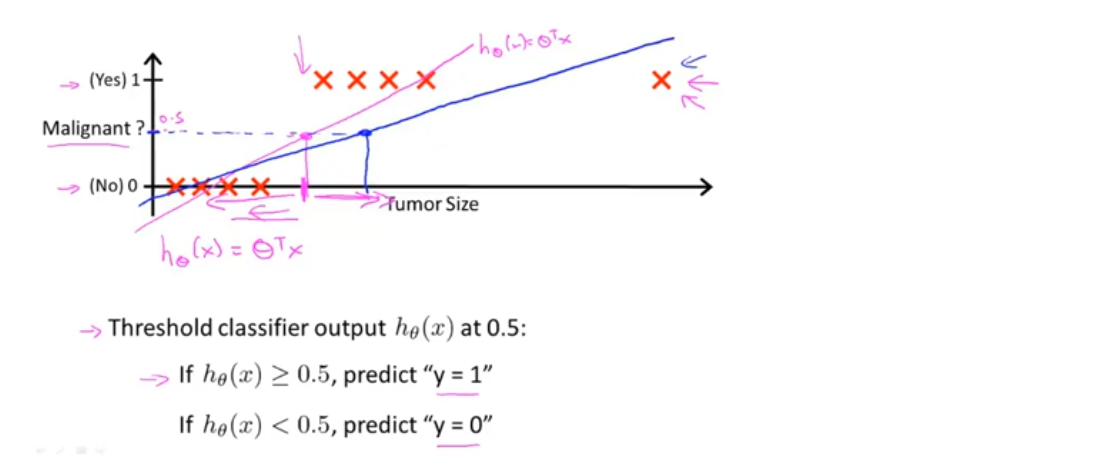
分类问题中(此节讨论二分类问题),y的取值为0和1,但线性回归的预测结果可能是远大于1,或远小于0
因此,将线性回归用于分类问题中是不合理的
逻辑回归:
预测值一直介于0,1之间
分类算法
假设陈述
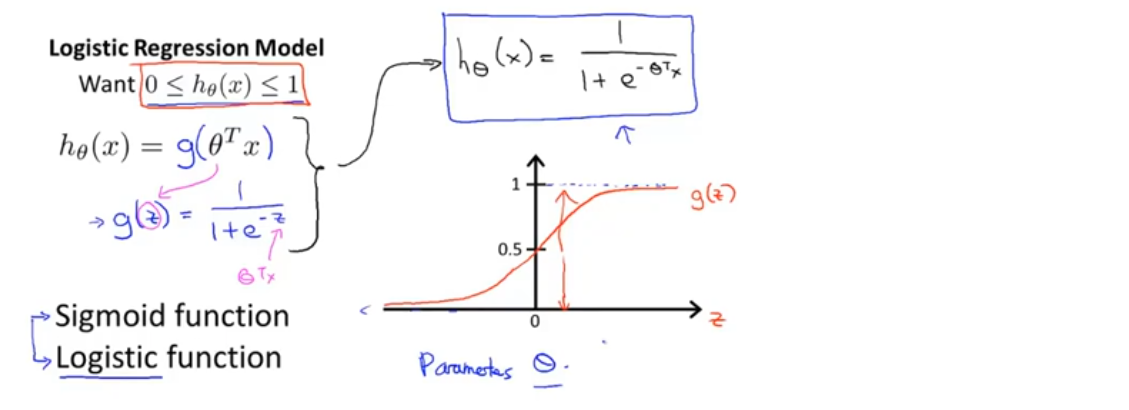
解释:h(x)的输出是,对于一个输入x,y=1的概率估计
决策界限
当θ^T x≥0时,预测y=1;当θ^T x<0时,预测y=0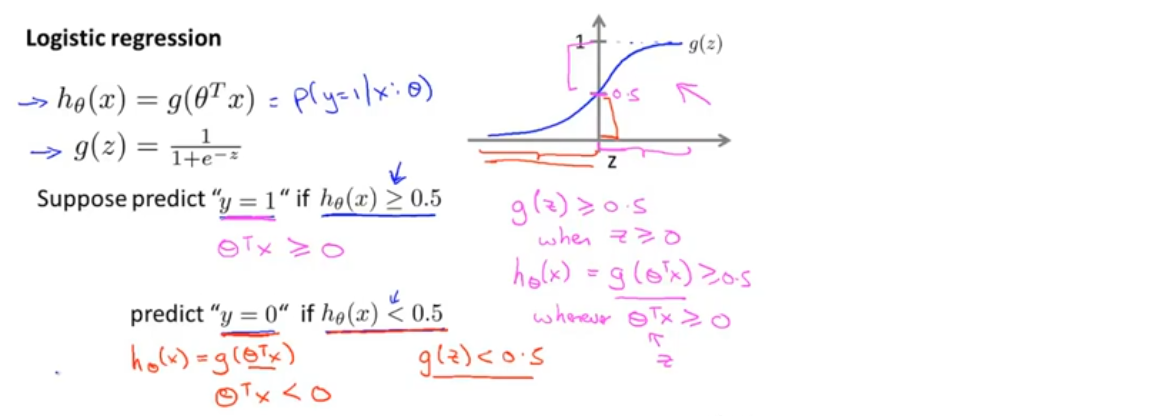
e.g.假设给定一个数据集,得出一个拟合好的逻辑回归函数,如下图所示
当-3+x1+x2≥0时,预测y=1;当-3+x1+x2<0时,预测y=0
-3+x1+x2=0这条直线叫做决策边界
决策边界是假设函数(hypothesis)的属性,取决于其参数,不是数据集的属性
非线性决策边界
e.g.假设给定一个数据集,得出一个拟合好的逻辑回归函数,如下图所示
代价函数

如果使用线性回归中的平方函数定义代价函数,得到的代价函数是非凸的(non-convex),因为h(x)是非线性的,这样就会有多个局部最优解,使用梯度下降法,无法保证得到全局最优解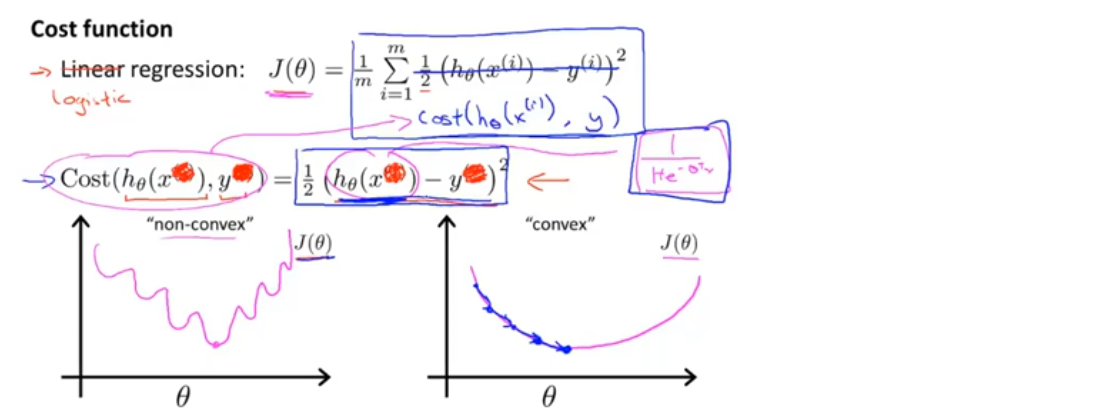
因此需要另找一个不同的代价函数,它是凸函数,使我们可以使用很好的算法,如梯度下降,能保证找到全局最小值
逻辑回归的代价函数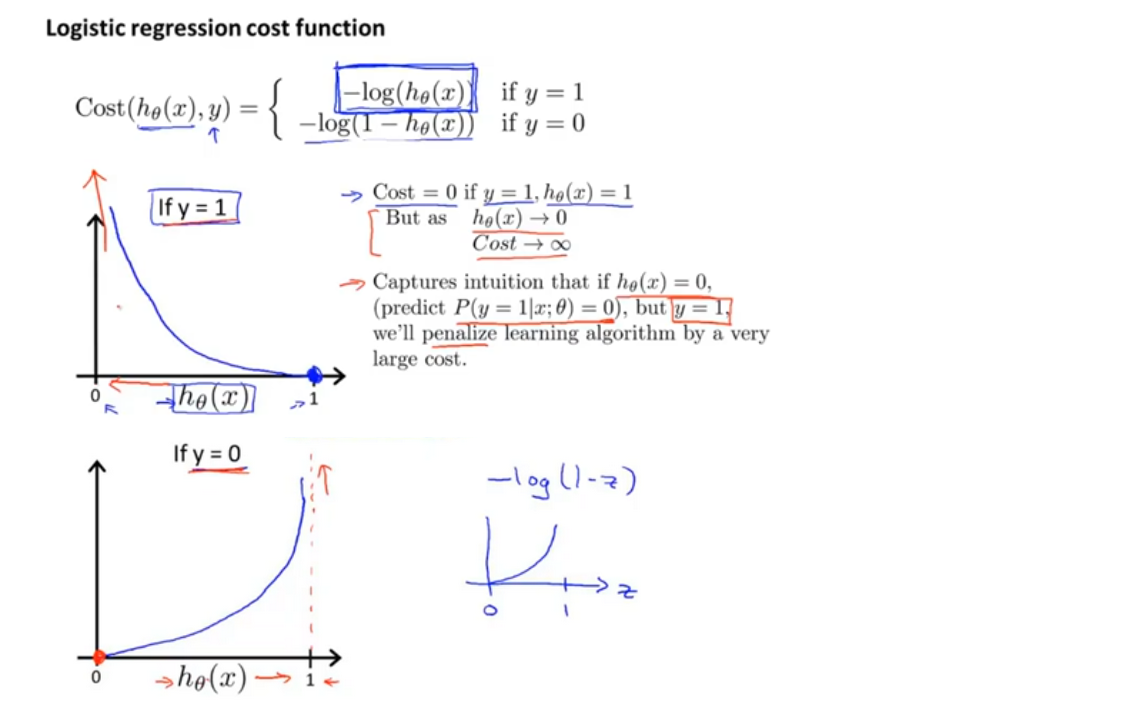
简化代价函数与梯度下降

逻辑回归的梯度下降规则,与线性回归的梯度下降规则,几乎一摸一样,但由于假设函数不同,其与线性回归的梯度下降是两个完全不同的东西
高级优化
介绍一些高级优化算法和高级优化概念,这些方法与梯度下降相比,能大大提高逻辑回归运行的速度,使算法更加适合解决大型的机器学习问题
其他优化算法:共轭梯度(Conjugate gradient),BFGS,L-BFGS
优点:
1、不需要手动选择α的值:这些算法给出计算导数项和代价函数的方法,可以理解为这些算法有一个智能内循环(clever inner-loop), 称为线搜索算法,它可以自动尝试不同的学习率α并自动选择一个好的学习率α,甚至可以为每次迭代选择不同的学习率
2、收敛得远远快于梯度下降:
缺点:更复杂
多元分类:一对多
一对多(一对余)的分类思想
假设给定一个训练集(如下图所示),其中包含三个类别,我们要做的是将这个训练集转化为三个独立的二分类问题,得到三个假设函数(分类器),分别输出y=i时的概率估计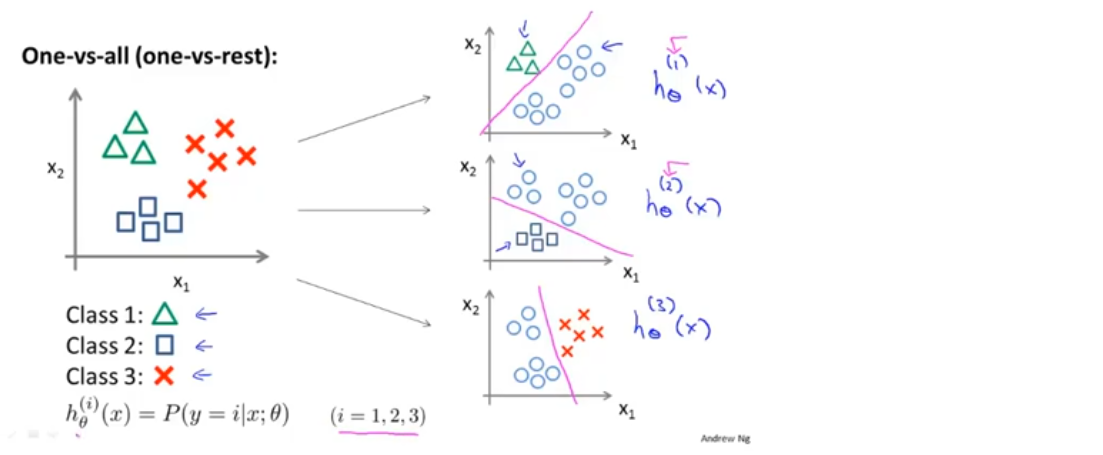
最后为了做出预测,给出一个新的输入值x,在三个分类器上运行,然后选择h最大的类别
也就是选择出三个中可信度最高、效果最好的分类器,无论i值是多少,都能得到一个最高的概率值,预测y就是那个i值