本节课内容:
1、多变量线性回归的Hypothesis公式、参数、代价函数。
2、特征缩放、归一化处理、以及学习率α值的选取。
3、特征的选取和多项式回归。
4、另外一种得到θ最优解的方法-正规方程,以及正规方程中X’X不可逆的情况和解决方法。
多变量线性回归
特征缩放(Feature Scaling)
不同特征的取值在相近的范围内,梯度下降法就能更快的收敛
e.g. 假设要根据房屋的面积和卧室的数量预测房屋的售价,房屋的面积取值范围是0-2000,卧室的数量的取值范围是1-5,画出代价函数的等值线(忽略θ_0),图形是很狭长的,这样在梯度下降找到全局最小时,需要很长的时间,且来回波动。
如果将特征进行缩放,把x_1 定义为房屋面积除以2000,把x_2 定义为卧室数量除以5,那么代价函数的等值线就不会很狭长,会更圆一点,在这样的代价函数上进行梯度下降,会找到一条更直接的路径通向全局最小
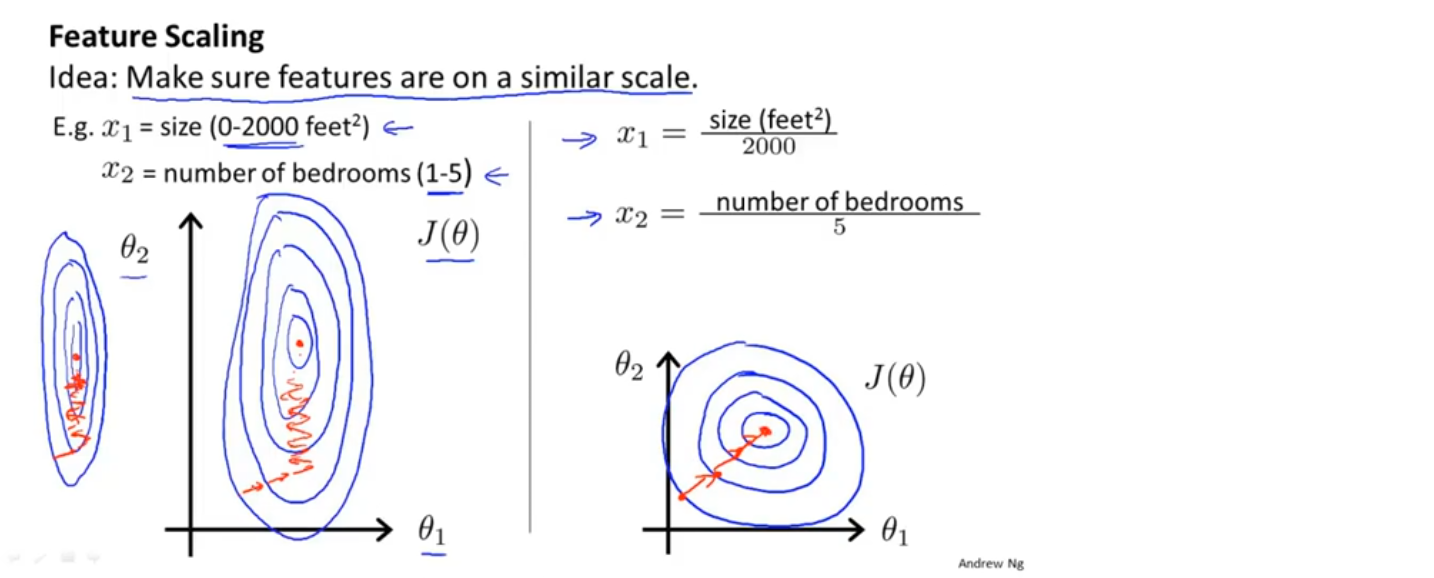
特征缩放是将特征的取值通过乘除限制在某个合适的范围内(不一定必须是-1~1之间),以使梯度下降更快的收敛,使迭代次数更少
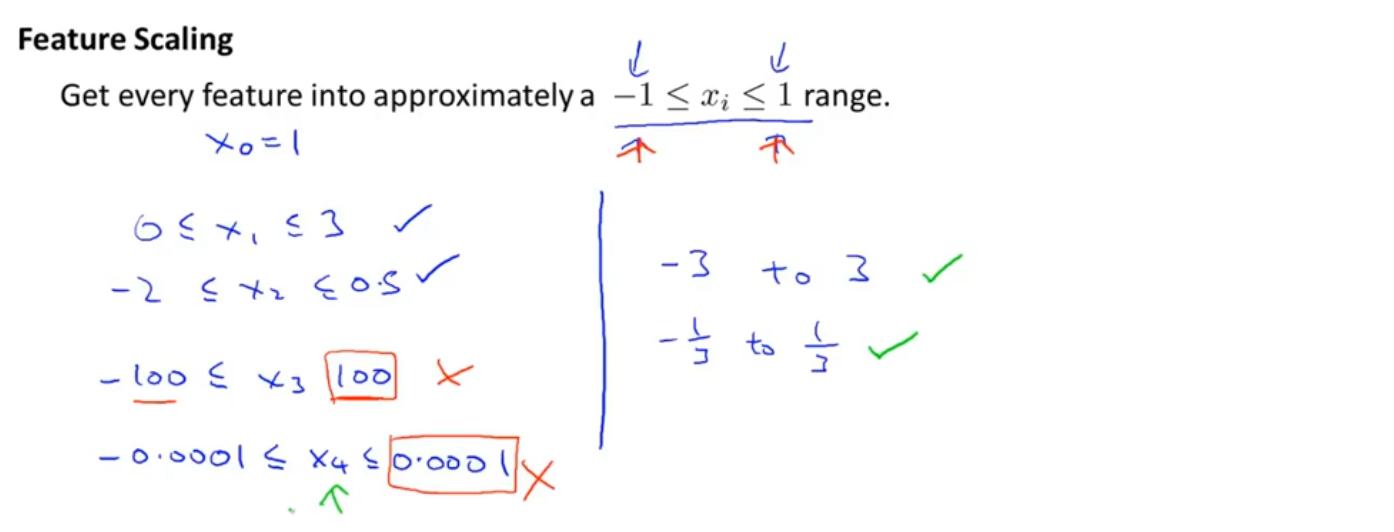
归一化处理
使用x_i−μ_i 代替x_i,使特征值取值的平均值为0
不用将归一化应用于特征x_0,因为x_0 的取值始终为1
将归一化和特征放缩相结合
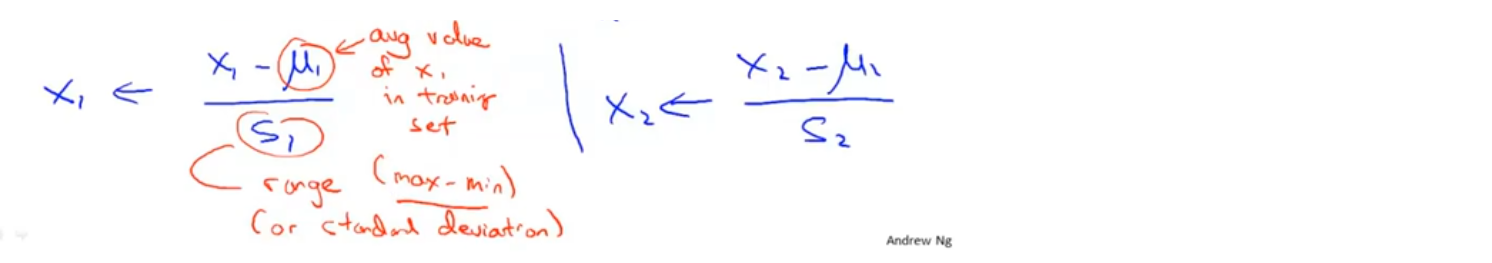
图中μ_i 的取值为特征值的平均值,s_i 的取值为特征值的范围(max-min)或者标准差
代价函数曲线
如果梯度下降算法正常工作,每一步迭代后的代价函数都应该下降
代价函数曲线可以判断是否收敛,以及梯度下降在迭代多少次后收敛
自动收敛测试:如果代价函数在一步迭代后的下降小于一个很小的值ϵ,即判断函数已经收敛
实际上,选择一个合适的阈值ϵ还是很困难的,所以(老师)更倾向于看代价函数曲线来判断收敛,而不是用自动收敛测试

代价函数也可以提前警告算法没有正常工作:
1、如果代价函数的值在不断上升,通常意味着应该使用较小的学习率α
最常见的原因是(代码中无错误的情况下),在尝试最小化一个碗型函数(图中粉色函数)时,学习率太大,梯度下降算法可能会不断冲过最小值
2、代价函数值不断的下降再升高,也是学习率α过大
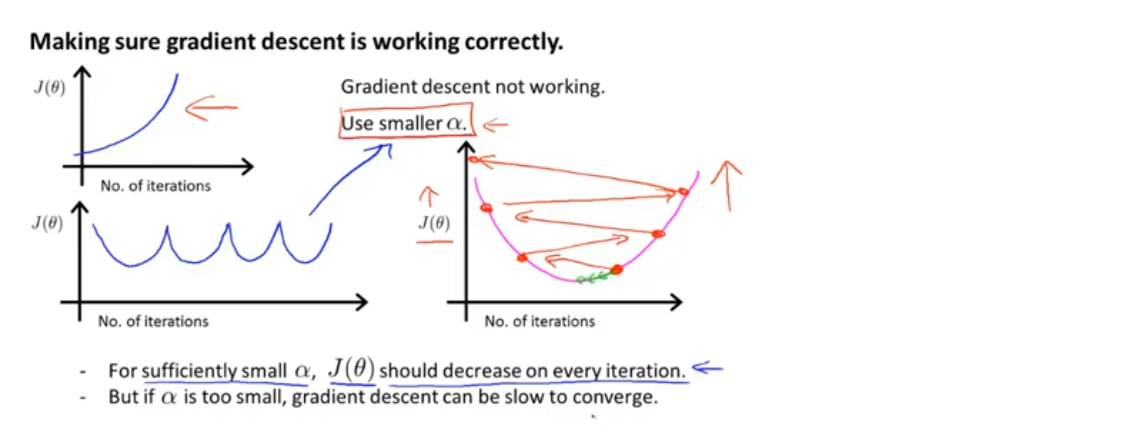
数学家已经证明,只要学习率α足够小,每次迭代后的代价函数都会下降
但如果学习率α取值非常小的话,梯度下降算法可能收敛的很慢
综上所述:
-如果学习率α取值非常小,梯度下降算法可能收敛的很慢
-如果学习率α取值非常大,代价函数可能在迭代后不下降;最后可能不收敛;也可能收敛很慢
通常选择α取值时,尝试一系列α值,直到找到一个使算法正常工作的最小的α值,和一个最大的α值,然后取最大的α值,或者比最大α值略小一点的比较合理的值

特征和多项式回归
1、特征:当使用线性回归时,不一定直接使用给出的特征,可以自己创造新的特征
e.g.给定的特征是房屋的宽度和深度,但我们可以选择将宽度和深度的乘积,即面积,作为特征
2、多项式回归:对于一个数据集,可能会有多个不同的模型进行拟合,当直线不能很好的拟合数据时,可以使用二次模型、三次模型等。可以使用多元线性回归的方法,对多元线性回归算法稍作修改,来实现二次模型、三次模型等。
3、当使用多项式回归时,特征放缩就变得更重要
4、凭着对各种函数图形到的了解,以及对数据形状的了解,通过选择不同的特征,可以得到更好的模型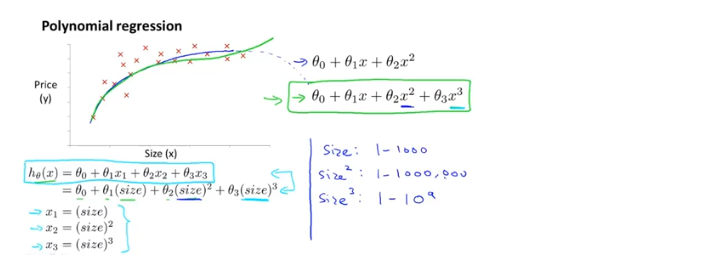
正规方程
一种求θ的解析解法,一次性求解θ的最优值,无需迭代
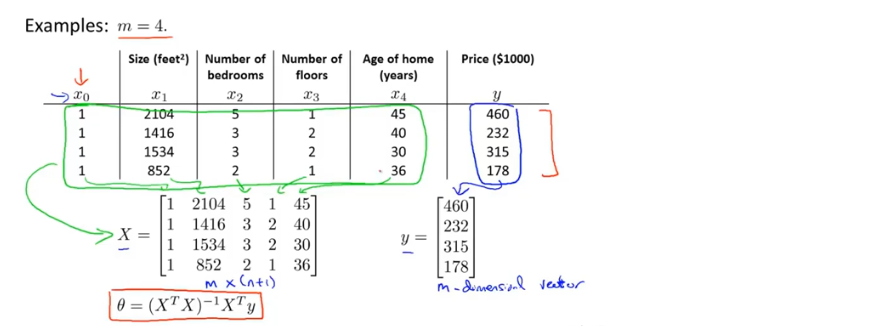

使用正规方程,不需要进行特征放缩
正规方程与梯度下降的优缺点:
当n较小时,选择正规方程;当n较大时,选择梯度下降,因为正规方程中求取逆矩阵的时间复杂度太高
正规方程不适合用于更复杂的学习算法中
正规方程中X’X不可逆的情况(X’为X的转置矩阵)
1、多余的特征(线性相关)
e.g.在预测房屋价格时,x1为房屋的面积(平方米),x2为房屋的面积(平方英尺),那么x1和x2之间存在一个线性关系,这时的特征矩阵X’X不可逆
2、特征太多(e.g.m≤n)
可以删除某些特征,或正则化
课程资料
课程原版PPT-Linear Algebra review (optional)
课程原版PPT-Linear Regression with multiple variables


